Introduction to Vectors

Definition of a vector

A vector is an object that has both a magnitude and a direction. Geometrically, we can picture a vector as a directed line segment, whose length is the magnitude of the vector and with an arrow indicating the direction. The direction of the vector is from its tail to its head.

Two vectors are the same if they have the same magnitude and direction. This means that if we take a vector and translate it to a new position (without rotating it), then the vector we obtain at the end of this process is the same vector we had in the beginning.

Two examples of vectors are those that represent force and velocity. Both force and velocity are in a particular direction. The magnitude of the vector would indicate the strength of the force or the speed associated with the velocity.

We denote vectors using boldface as in a$\mathbf{a}$ or b$\mathbf{b}$. Especially when writing by hand where one cannot easily write in boldface, people will sometimes denote vectors using arrows as in a⃗ $\overrightarrow{a}$ or b⃗ $\overrightarrow{b}$, or they use other markings. We won't need to use arrows here. We denote the magnitude of the vector a$\mathbf{a}$ by ∥a∥$\parallel \mathbf{a}\parallel$. When we want to refer to a number and stress that it is not a vector, we can call the number a scalar. We will denote scalars with italics, as in a$a$ or b$b$.

You can explore the concept of the magnitude and direction of a vector using the below applet. Note that moving the vector around doesn't change the vector, as the position of the vector doesn't affect the magnitude or the direction. But if you stretch or turn the vector by moving just its head or its tail, the magnitude or direction will change.

You may use this link to show the applet 

The magnitude and direction of a vector. The blue arrow represents a vector a$\mathbf{a}$. The two defining properties of a vector, magnitude and direction, are illustrated by a red bar and a green arrow, respectively. The length of the red bar is the magnitude ∥a∥$\parallel \mathbf{a}\parallel$ of the vector a$\mathbf{a}$. The green arrow always has length one, but its direction is the direction of the vector a$\mathbf{a}$. 

You can change either end of a$\mathbf{a}$ by dragging it with your mouse. You can also move a$\mathbf{a}$ by dragging the middle of the vector; however, changing the position of the a$\mathbf{a}$ in this way does not change the vector, as its magnitude and direction remain unchanged.

We can define a number of operations on vectors geometrically without reference to any coordinate system. Here we define addition, subtraction, and multiplication by a scalar. On separate pages, we discuss two different ways to multiply two vectors together: the dot product and the cross product.

Addition of vectors

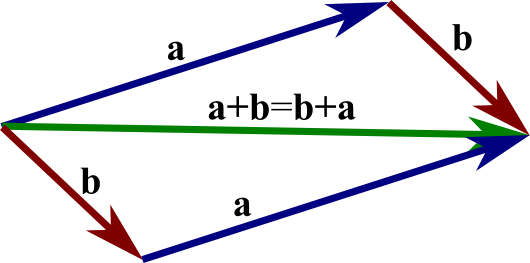
Given two vectors a$\mathbf{a}$ and b$\mathbf{b}$, we form their sum a+b$\mathbf{a}+\mathbf{b}$, as follows. We translate the vector b$\mathbf{b}$ until its tail coincides with the head of a$\mathbf{a}$. (Recall such translation does not change a vector.) Then, the directed line segment from the tail of a$\mathbf{a}$ to the head of b$\mathbf{b}$ is the vector a+b$\mathbf{a}+\mathbf{b}$.

The vector addition is the way forces and velocities combine. For example, if a car is travelling due north at 20 miles per hour and a child in the back seat behind the driver throws an object at 20 miles per hour toward his sibling who is sitting due east of him, then the velocity of the object (relative to the ground!) will be in a north-easterly direction. The velocity vectors form a right triangle, where the total velocity is the hypotenuse. Therefore, the total speed of the object (i.e., the magnitude of the velocity vector) is 202+202−−−−−−−−√=202√$\sqrt{{20}^2+{20}^2}=20\sqrt{2}$ miles per hour relative to the ground.

Addition of vectors satisfies two important properties.

1. The commutative law, which states the order of addition doesn't matter:

   a+b=b+a.$$\mathbf{a}+\mathbf{b}=\mathbf{b}+\mathbf{a}.$$
   This law is also called the parallelogram law, as illustrated in the below image. Two of the edges of the parallelogram define a+b$\mathbf{a}+\mathbf{b}$, and the other pair of edges define b+a$\mathbf{b}+\mathbf{a}$. But, both sums are equal to the same diagonal of the parallelogram.

   

2. The associative law, which states that the sum of three vectors does not depend on which pair of vectors is added first:

   (a+b)+c=a+(b+c).$$(\mathbf{a}+\mathbf{b})+\mathbf{c}=\mathbf{a}+(\mathbf{b}+\mathbf{c}).$$

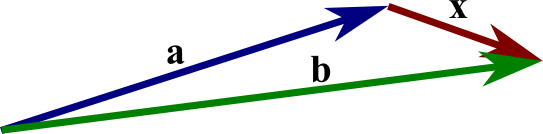
Vector subtraction

Before we define subtraction, we define the vector −a$-\mathbf{a}$, which is the opposite of a$\mathbf{a}$. The vector −a$-\mathbf{a}$ is the vector with the same magnitude as a$\mathbf{a}$ but that is pointed in the opposite direction.

We define subtraction as addition with the opposite of a vector: